Vclass Pertemuan 2 (Peng. Teknologi Sistem Cerdas #)

Contoh Latihan Teknik Pencarian Generate and Test :

Pencarian dilakukan dari titik A menuju titik C dengan daftar trayek :

- 1A melewati halte: A , D, dan C

- 2A melewati halte : A, E, D, dan C

- 1B melewati halte : B dan D

- 2B melewati halte : A dan B

- 3A melewati halte : B, C dan E

Waktu jeda 1A = 5 menit, 1B = 5 menit, 2A = 7 menit, 2B = 10 menit, dan 3A = 7 menit.

Daftar waktu yang dibutuhkan adalah :

A – B = 8 menit B – D = 7 menit

A – D = 5 menit D – C = 8 menit

A – E = 5 menit E – B = 3 menit

B – C = 7 menit E – D = 5 menit

Berikut ini adalah langkah-langkah penyelesaian kasus di atas adalah :

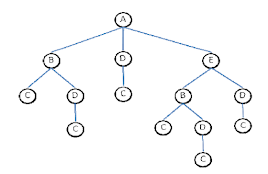
1. Menjabarkan satu per satu kemungkinan yang ada. Gambar 5 menggambarkan proses penjabaran satu per satu kemungkinan yang ada.

2. Membuat daftar tabel beserta perhitungan jarak dan waktu untuk setiap jalur yang telah dilewati.

Tabel 1 Alur Pencarian Jarak

Tabel 2 Alur Pencarian Waktu

3. Dari Tabel 1 ditemukan rute terpendek berdasarkan jarak adalah A – D – C dengan total jarak 10 km. Rute alternatif 1 adalah A – B – C dengan total jarak 11 km. Rute alternatif 2 adalah A – E – B – C dengan total jarak 11 km.

4. Dari Tabel 2 ditemukan rute terpendek berdasarkan waktu adalah A – D – C dengan total waktu 13 menit. Rute alternatif 1 adalah A – B – C dengan total waktu 15 menit. Rute alternatif 2 adalah A – E – B – C dengan total waktu 15 menit.

5. Setelah melakukan perhitungan jarak dan waktu, langkah selanjutnya adalah menentukan trayek bus yang digunakan pada masing-masing rute. Tabel 3 menunjukkan penentuan trayek pada masing – masing rute.

Tabel 3 Penentuan Trayek

Berdasarkan analisis perhitungan yang dilakukan maka rute terpendek berdasarkan jarak adalah A – D – C dengan total jarak tempuh 10 km tanpa perpindahan.

Berdasarkan analisis perhitungan yang dilakukan maka rute terpendek berdasarkan waktu adalah A – D – C dengan total waktu tempuh 13 menit tanpa perpindahan trayek.

Contoh Latihan Teknik Pencarian Hill Climbing :

Ruang keadaan berisi semua kemungkinan lintasan yang mungkin. Operator digunakan untuk menukar posisi kota yang bersebelahan. Apabila ada n kota dan ingin mencari kombinasi lintasan maka dengan cara menukar posisi urutan 2 kota, n kombinasi 2.

Kombinasi yang didapat sebanyak 6 kombinasi atau dengan menggunakan rumus :

• Panjang lintasan yang dihasilkan dari fungsi heuristic = 12

• Tahapan heuristic 6 kombinasi = level 5

• Jalur lintasan yang dipilih dengan fungsi heuristik = DBCA